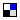Acceleration curve vs torque curve vs HP curve.
#1
Hey,
So heres this interesting question that few can agree on, and I'm sure people here can lay the maths down.
If you take a dyno sheet with power and torque curves, and you lay an acceleration curve over it for the same car in the same gear dyno tested, and account for friction (including air resistance) then does the acceleration curve follow the torque curve or the power curve.
Here is what I know:
Horsepower is work/time.
Torque is force per revolution. The VE curve roughly follows the torque curve, but frictional losses and the combustion efficiency leaves some variation.
Higher torque=higher force per revolution through the drivetrain AND at the wheels.
The confusing part is that higher horsepower is greater energy output per second, so while torque may drop off as revs rise the frequency of the torque output is increased.
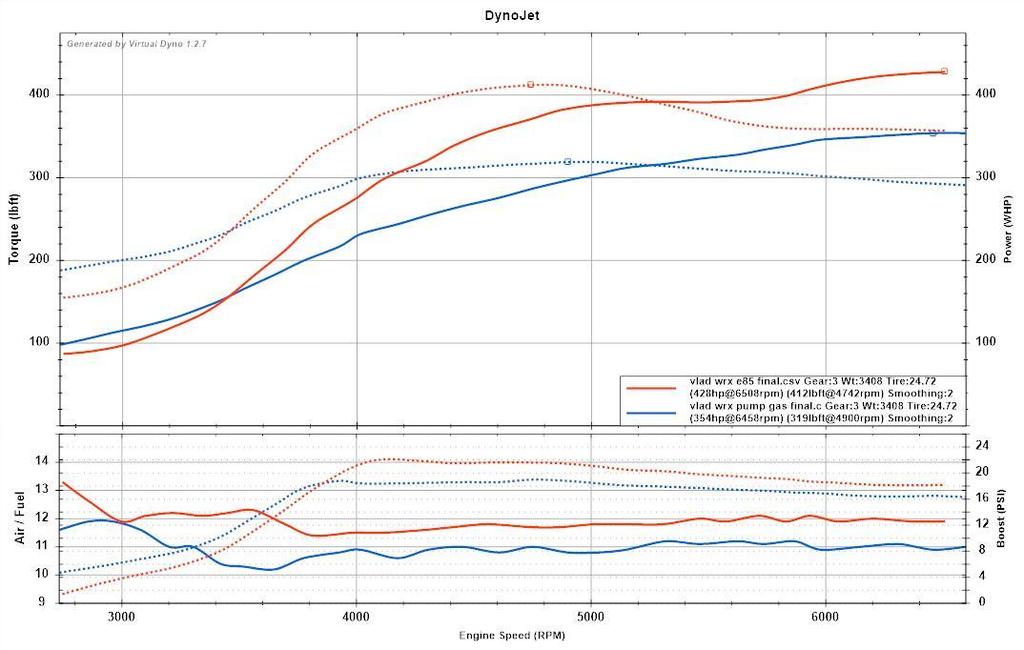
Take this randomly googled dyno sheet for example, we can see torque drop off from 4500rpm, so VE and therefore force per cycle is decreasing as RPM rises, but HP remains pretty flat because the cycles per second (rpm) is increasing at the same rate that torque is dropping off.
What I really want is for someone to actually lay acceleration data over a dyno sheet.
Im not going to put what I believe down, I want other people who know the maths to school me with real data.
Thankyou,
Dann
So heres this interesting question that few can agree on, and I'm sure people here can lay the maths down.
If you take a dyno sheet with power and torque curves, and you lay an acceleration curve over it for the same car in the same gear dyno tested, and account for friction (including air resistance) then does the acceleration curve follow the torque curve or the power curve.
Here is what I know:
Horsepower is work/time.
Torque is force per revolution. The VE curve roughly follows the torque curve, but frictional losses and the combustion efficiency leaves some variation.
Higher torque=higher force per revolution through the drivetrain AND at the wheels.
The confusing part is that higher horsepower is greater energy output per second, so while torque may drop off as revs rise the frequency of the torque output is increased.
Take this randomly googled dyno sheet for example, we can see torque drop off from 4500rpm, so VE and therefore force per cycle is decreasing as RPM rises, but HP remains pretty flat because the cycles per second (rpm) is increasing at the same rate that torque is dropping off.

What I really want is for someone to actually lay acceleration data over a dyno sheet.
Im not going to put what I believe down, I want other people who know the maths to school me with real data.
Thankyou,
Dann
Last edited by nitrodann; 02-27-2016 at 06:45 PM.
#2
The answer is, maximize torque to the wheels at all times.
So if reving the engine higher in the current gear/current speed (vs shifting to the next gear) results in more torque TO THE WHEELS, then staying in that gear is better. This is independent of weight/drag/etc. Whatever maximizes torque to the wheels will result in maximum acceleration.
So if reving the engine higher in the current gear/current speed (vs shifting to the next gear) results in more torque TO THE WHEELS, then staying in that gear is better. This is independent of weight/drag/etc. Whatever maximizes torque to the wheels will result in maximum acceleration.
#6
It's torque at the wheels what counts. Just like Pat said. Torque @ wheels is torque @ engine x total gearing x drivetrain efficiency.
No overlays of graphs needed. It's basic physics: f= m x a
=> a = f/m
assuming that m is constant, we get:
a ~ f
the force the wheels exert is equal to torque at the wheel divided by wheel radius.
So on a car with a somewhat adequate gearbox, it's hp, not torque.
One caveat: the force the wheels transmit not only has to accelerate the car, but also overcome all resistances like aerodynamic drag and roll resistance.
No overlays of graphs needed. It's basic physics: f= m x a
=> a = f/m
assuming that m is constant, we get:
a ~ f
the force the wheels exert is equal to torque at the wheel divided by wheel radius.
So on a car with a somewhat adequate gearbox, it's hp, not torque.
One caveat: the force the wheels transmit not only has to accelerate the car, but also overcome all resistances like aerodynamic drag and roll resistance.
#8
If you took your car out, and measured longitudinal g during an acceleration run through a single gear, from idle to redline the resulting graph would mirror the torque curve. With peak acceleration happening at whatever speed corresponded to the rpm of the torque peak.
If you happen to choose a high gear, 4th or 5th say, then yes aero drag will distort the picture some, or maybe even a lot.
BUT, and this is important, you specified "in the same gear". The real question is what is the maximum acceleration you can achieve at a given speed, and in that case you want to use the gear that puts you closest to the power peak, not the torque peak.
Using the dyno chart you posted, you have a torque peak of 240ftlbs at 4400 rpm
and a power peak of 230hp at 5900 rpm. Torque at 5900 rpm is about 205.
So for any given speed the difference in gear ratio between the engine being at the power peak vs the torque peak is 5900/4400 or 1.34. Meaning that due to gearing we multiply the torque times 1.34 for the engine at peak power vs the torque peak. 205 * 1.34 = 274. 274 is more than 240.
If you happen to choose a high gear, 4th or 5th say, then yes aero drag will distort the picture some, or maybe even a lot.
BUT, and this is important, you specified "in the same gear". The real question is what is the maximum acceleration you can achieve at a given speed, and in that case you want to use the gear that puts you closest to the power peak, not the torque peak.
Using the dyno chart you posted, you have a torque peak of 240ftlbs at 4400 rpm
and a power peak of 230hp at 5900 rpm. Torque at 5900 rpm is about 205.
So for any given speed the difference in gear ratio between the engine being at the power peak vs the torque peak is 5900/4400 or 1.34. Meaning that due to gearing we multiply the torque times 1.34 for the engine at peak power vs the torque peak. 205 * 1.34 = 274. 274 is more than 240.
#9
I dislike torque. It's a great visual representation of the low-end power of an engine, but not much else. Power is much simpler.
For a given road speed, you can have an engine making 200ft.lbs at 5252rpm. You can have another engine making 100ft.lbs at 10504rpm, but in order to maintain the same road speed at that RPM, you need twice as much total gear reduction, so the output torque is the same.
Or, you can look at the power curve, and see that both engines are making 200whp at their respective RPMs, and just compare with that.
For a given road speed, you can have an engine making 200ft.lbs at 5252rpm. You can have another engine making 100ft.lbs at 10504rpm, but in order to maintain the same road speed at that RPM, you need twice as much total gear reduction, so the output torque is the same.
Or, you can look at the power curve, and see that both engines are making 200whp at their respective RPMs, and just compare with that.

#10
If you lay acceleration over a dyno graph, the acceleration would mirror torque. Unfortunately, if you use just this measurement, you'll be fooled into thinking that torque is the important number; this is because you can obviously see that if torque is halved, then so is acceleration. What you fail to see as obvious is what happens when RPMs are halved.
Consider an engine that produces a perfectly flat 100 ft lbs of torque and red-lines at 5252 rpm. By simple math, we can deduce that at red line, this engine is producing exactly 100 hp. Now consider an arbitrary 0-100mph acceleration using said 100 ft lbs car.
Now consider what would happen if we placed an artificial rev limiter at 2626 rpm on that same engine. You'll quickly note that we have in no way changed the torque output of the engine, but when we do the maths this time, we come up with a red-line hp of exactly 50 hp. Run through the same 0-100mph test with this same car in the new configuration - you'll feel as though you're short shifting every gear because that's as fast as the engine is allowed to run - first gear in both cars will accelerate at the same rate, so will second and third and...all the way up to 6 - but here's the important part - the top speed in each gear is exactly half of what it was. If first gear at full RPMs goes up to 30mph, then first gear at half RPMs only goes to 15mph. We must then consider the difference of the acceleration between the two cars between 15 mph and 30 mph. Recall, their torque curves are exactly the same, but which car accelerates quicker from 15 to 30? Every time it will be the 100hp car instead of the 50hp car. This is because torque to the wheels is not directly determined by the engine, but rather by the gearing. Only *power* is determined by the engine.
If you really want to get into the weeds on this, consider my following example: you live in a magical world where we have no driveline losses and centripetal force doesn't destroy mechanical bits. You have two cars that, except for the engine/transmission are otherwise identical. Car A has a 10hp lawnmower engine in it, but it produces that 10hp with only 1 foot pound of torque (at a 52,520 rpm redline). Car B is a 500 ft-lb behemoth, but it can only manage enough RPMs (about 10.5 rpm) to generate 1hp.
Each car is set up with a 1-speed transmission that allows the cars to drive at exactly 30mph at redline - we'll consider a tire speed of about 350 RPMs to achieve 30mph (approximately 30" tire circumference).
In order for the lawnmower engine to drive the car at 350 RPMs, the transmission must be geared way down. 52,520 / 350 = about 150 - so this car will be geared down at a ratio of 150:1 to achieve suitable rear wheel RPMs to redline at 30mph.
The beastly engine needs to be geared up - 350/10.5 = about 33.33 - we'll have to gear this engine up at a ratio of 1:33.33 to achieve 30mph.
Once our weedeater engine is geared down which increases torque at the cost of RPMs, the final torque at the rear wheels is 1*150 - or 150 rwtq - all the way from 0mph to 30mph on its single-speed "transmission".
Our 500hp tq engine has to be geared up, which gains RPMs at the cost of torque, the final torque at the rear wheels is 500 / 33.33 - or 15 rwtq - all the way from 0mph to 30mph.
You've probably already noticed that the torquey engine has exactly 1/10th the torque as the gutless engine in our 30mph top speed test - you are also considering that the torquey engine also had exactly 1/10th the horsepower as the gutless engine. Coincidence? Absolutely not. This is because engine HP (not engine torque) is is the best measurement for ideal car acceleration.
Certainly in this case, it will be the torque - 150ft-lb versus 15ft-lb which gets the lawnmower-engined car up to 30 mph far quicker than the behemoth 500 ft-lb engine - but it's wheel torque that counts when accelerating - and engine speed is easily converted to wheel torque using those simple things we call gears.
Even if we add in a multi-gear transmission, that 500wtq beast will still be a dog compared to the 10hp lawnmower-engined car.
Now, lets get back to our non-ideal world. In our non-ideal world torque curves are not perfectly flat horizontal line segments which you could play a game of marbles on, but rather they're bumpy, curvy, finicky things - and occasionally you get toyota-supra dyno-queen HP curves that are 1hp...1hp....1hp....1hp...1hp...2hp....4hp...WTFOM G63GAZILLIONhp.
Yes, this is a case where a car with WTFOMG63GAZILLIONhp is going to be an absolute dog - so not all HP curves are created equal, but as a rule of thumb, a higher HP car will generally out-accelerate a lower HP car. What's more important perhaps is how to use integrals to determine what "horsepower" really wants to tell you - your final answer, perhaps on what really is the important thing to consider, is this: With all things being equal, the car that will win every single acceleration competition is the one with the most area underneath the torque curve. Just make sure that you remember that area is a measurement of both the height AND the length of the torque curve - RPMs count just as much as the actual torque value.
Consider an engine that produces a perfectly flat 100 ft lbs of torque and red-lines at 5252 rpm. By simple math, we can deduce that at red line, this engine is producing exactly 100 hp. Now consider an arbitrary 0-100mph acceleration using said 100 ft lbs car.
Now consider what would happen if we placed an artificial rev limiter at 2626 rpm on that same engine. You'll quickly note that we have in no way changed the torque output of the engine, but when we do the maths this time, we come up with a red-line hp of exactly 50 hp. Run through the same 0-100mph test with this same car in the new configuration - you'll feel as though you're short shifting every gear because that's as fast as the engine is allowed to run - first gear in both cars will accelerate at the same rate, so will second and third and...all the way up to 6 - but here's the important part - the top speed in each gear is exactly half of what it was. If first gear at full RPMs goes up to 30mph, then first gear at half RPMs only goes to 15mph. We must then consider the difference of the acceleration between the two cars between 15 mph and 30 mph. Recall, their torque curves are exactly the same, but which car accelerates quicker from 15 to 30? Every time it will be the 100hp car instead of the 50hp car. This is because torque to the wheels is not directly determined by the engine, but rather by the gearing. Only *power* is determined by the engine.
If you really want to get into the weeds on this, consider my following example: you live in a magical world where we have no driveline losses and centripetal force doesn't destroy mechanical bits. You have two cars that, except for the engine/transmission are otherwise identical. Car A has a 10hp lawnmower engine in it, but it produces that 10hp with only 1 foot pound of torque (at a 52,520 rpm redline). Car B is a 500 ft-lb behemoth, but it can only manage enough RPMs (about 10.5 rpm) to generate 1hp.
Each car is set up with a 1-speed transmission that allows the cars to drive at exactly 30mph at redline - we'll consider a tire speed of about 350 RPMs to achieve 30mph (approximately 30" tire circumference).
In order for the lawnmower engine to drive the car at 350 RPMs, the transmission must be geared way down. 52,520 / 350 = about 150 - so this car will be geared down at a ratio of 150:1 to achieve suitable rear wheel RPMs to redline at 30mph.
The beastly engine needs to be geared up - 350/10.5 = about 33.33 - we'll have to gear this engine up at a ratio of 1:33.33 to achieve 30mph.
Once our weedeater engine is geared down which increases torque at the cost of RPMs, the final torque at the rear wheels is 1*150 - or 150 rwtq - all the way from 0mph to 30mph on its single-speed "transmission".
Our 500hp tq engine has to be geared up, which gains RPMs at the cost of torque, the final torque at the rear wheels is 500 / 33.33 - or 15 rwtq - all the way from 0mph to 30mph.
You've probably already noticed that the torquey engine has exactly 1/10th the torque as the gutless engine in our 30mph top speed test - you are also considering that the torquey engine also had exactly 1/10th the horsepower as the gutless engine. Coincidence? Absolutely not. This is because engine HP (not engine torque) is is the best measurement for ideal car acceleration.
Certainly in this case, it will be the torque - 150ft-lb versus 15ft-lb which gets the lawnmower-engined car up to 30 mph far quicker than the behemoth 500 ft-lb engine - but it's wheel torque that counts when accelerating - and engine speed is easily converted to wheel torque using those simple things we call gears.
Even if we add in a multi-gear transmission, that 500wtq beast will still be a dog compared to the 10hp lawnmower-engined car.
Now, lets get back to our non-ideal world. In our non-ideal world torque curves are not perfectly flat horizontal line segments which you could play a game of marbles on, but rather they're bumpy, curvy, finicky things - and occasionally you get toyota-supra dyno-queen HP curves that are 1hp...1hp....1hp....1hp...1hp...2hp....4hp...WTFOM G63GAZILLIONhp.
Yes, this is a case where a car with WTFOMG63GAZILLIONhp is going to be an absolute dog - so not all HP curves are created equal, but as a rule of thumb, a higher HP car will generally out-accelerate a lower HP car. What's more important perhaps is how to use integrals to determine what "horsepower" really wants to tell you - your final answer, perhaps on what really is the important thing to consider, is this: With all things being equal, the car that will win every single acceleration competition is the one with the most area underneath the torque curve. Just make sure that you remember that area is a measurement of both the height AND the length of the torque curve - RPMs count just as much as the actual torque value.
#11
Fact. Torque is a useless figure worshiped by the murican muscle crowd to compare short epeens. I see that all the time around the mustang crowd. "oh but it's got 300 pounds of torque" Make that 300 pounds of torque at 7k rpm then we can talk.
For racing purposes, you dont care what your max torque per engine revolution is. You care strictly about the combined power of all cylinders at the appropriate rpm. aka HP.
For example. less than 250ft.lb.
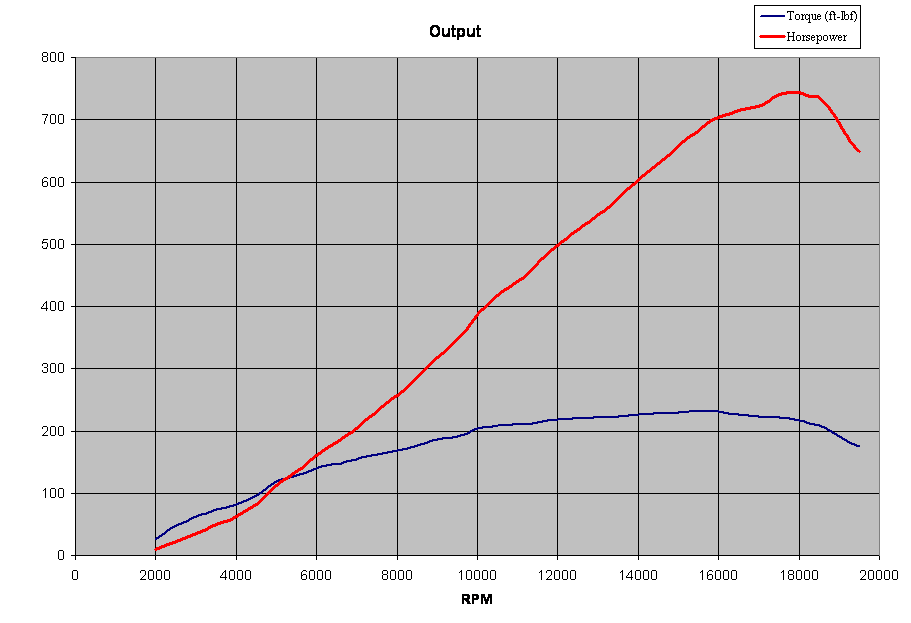
For racing purposes, you dont care what your max torque per engine revolution is. You care strictly about the combined power of all cylinders at the appropriate rpm. aka HP.
For example. less than 250ft.lb.

#13
Mathematics is great, but unless there is a real world application, it's just mathematics. To me it's completely useless to know that I can take a hamster running in a wheel and use a series of gears/pulleys to pull a 200lb human in a wagon. Similarly, theorizing on the use of impractical and impossible gearing options for a vehicle, it doesn't matter to me if I can take two extremely different motors and manipulate the work output by gearing.
Here's a real world example. If both the graph I posted and the graph above are a Miata with the same weight and gearing and assuming no traction limitations, my Miata wins the acceleration contest - at least to a reasonable speed. And I think that in the world we are discussing this, we are concerned with off corner acceleration up to such a reasonable speed.
Here's a real world example. If both the graph I posted and the graph above are a Miata with the same weight and gearing and assuming no traction limitations, my Miata wins the acceleration contest - at least to a reasonable speed. And I think that in the world we are discussing this, we are concerned with off corner acceleration up to such a reasonable speed.
#14
Pretty good article. Spoiler from the last paragraph.
"torque applied for a large range of rpms
equates to faster acceleration"
Yet another guide to Torque versus Horsepower versus Acceleration
"torque applied for a large range of rpms
equates to faster acceleration"
Yet another guide to Torque versus Horsepower versus Acceleration
#16
Maximize torque at all rpms, everything else that follows is bonus. I care less about horsepower when discussing miata, only torques.
1.6 and 1.8 don't last revving higher than 7K, so that's the limiting factor for 99.9% of us. More torque at the same revs, more power, more fast.
I don't even understand this thread.
1.6 and 1.8 don't last revving higher than 7K, so that's the limiting factor for 99.9% of us. More torque at the same revs, more power, more fast.
I don't even understand this thread.
#17
Pretty good article. Spoiler from the last paragraph.
"torque applied for a large range of rpms
equates to faster acceleration"
Yet another guide to Torque versus Horsepower versus Acceleration
"torque applied for a large range of rpms
equates to faster acceleration"
Yet another guide to Torque versus Horsepower versus Acceleration
He also fails to suggest that on his 200 ft-lb engine with a 200 lb rock suspended on a 1-ft radius flywheel, the engine itself is incapable of accelerating the rock upward, as the upward pull of the engine would equal the downward pull of gravity on the rock. It would simply sit suspended unless something helped the rock first accelerate upward, at which point the engine would slowly begin hoisting said rock at a constant rate of speed equal to the assistance provided by the external factor.
In fact, in no example he provides (save the geared example, using 1st gear from 0-500 rpms) will the engine actually be capable of providing upward acceleration of the rock.
I have no qualms with the assumption that the rope must have no mass; this is, after all, an "idealized" concept.